
Some may think that put-call parity in options is just a theoretical concept with no practical applications, as arbitrage opportunities are unavailable to retail traders.
We will show you how it has practical application in constructing risk-free trades.
And we are not talking about arbitrage.
We had shown previously with the risk-free collar that risk-free trades are indeed possible.
Today, we show a different variation that might be aptly named the risk-free butterfly collar.
Contents
In a previous video, we discussed how one can engage in options trading without incurring a loss of capital in a portfolio.
This is because we can receive risk-free interest from U.S. Treasury bills.
It is these risk-free interest returns that enable risk-free trading to be possible.
If the interest received is more than the defined max risk of the trade, then you have a risk-free trade.
The risk-free interest rate is already factored into the prices of options contracts.
Just look at the Black-Scholes options pricing model:
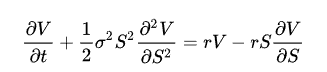
Source: Wikipedia
It has the risk-free interest rate “r” as one of its inputs.
As a practical application, we will construct a risk-free trade that harnesses the free money that is embedded in certain stock and options derivative combinations.
But first, we need to know what put-call parity is.
Put-call parity means that the price of the call option and the price of the put option (for the same strike and expiration) are intimately linked.
As the underlying asset price goes up, the call option increases in value.
The put option (of the same strike, expiration, and underlying) must synchronously decrease in value.
And vice versa.
It is possible to derive the price of the put option by knowing the price of the call option.
And vice versa.
Because the two prices must obey this formula:
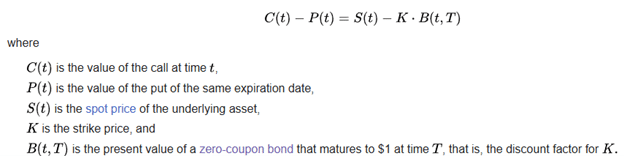
The last term is the present value of a zero-coupon bond. U.S. Treasury bills are one type of zero-coupon bond, which earns a risk-free rate of return.
Again, we see “free money” entering the equation.
Because if the price of the call and the price of the put option do not obey this formula, there would be an arbitrage opportunity.
In practice, arbitrage opportunities are scarce because the market is highly efficient, and algorithmic trading helps keep prices in line.
However, we are not here to engage in arbitrage.
Put-call parity enables us to construct synthetic positions.
For example,
Long call = long stock + long put
This means that having a long call option is equivalent to owning 100 shares of the underlying asset and holding a long put option with the same strike and expiration.
Suppose Investor Adam buys a 560-strike call option on QQQ expiring in 34 days on September 26, 2025.
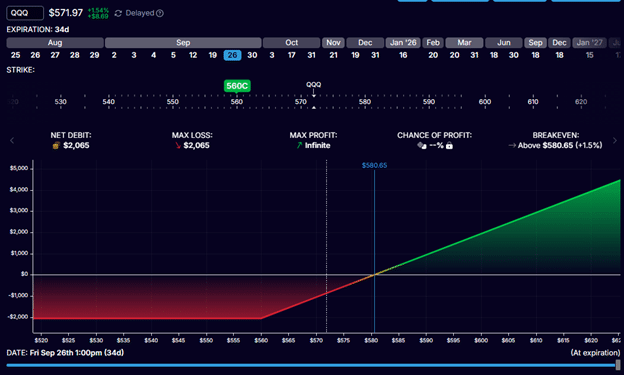
Investor Adam paid $2065 to buy this call option, and that would be the maximum possible loss.
Investor Betty initiates an equivalent position by buying 100 shares of QQQ and buying a put option of the same strike and expiration:
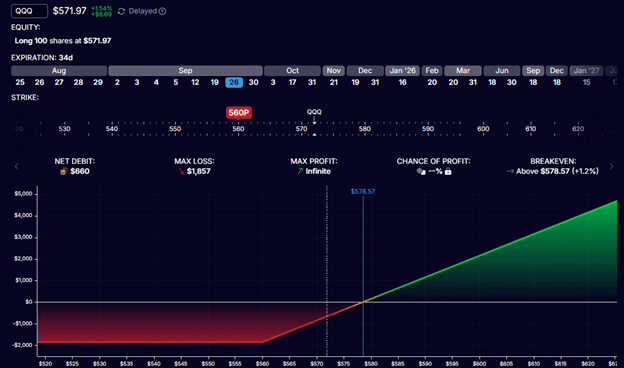
Cost of 100 shares of QQQ: -$57,197
Cost of 560-put option: -$660
Net debit: -$57,857
Whereas Investor Adam paid $2065, Investor Betty paid $57,857 for an alternative position that has a similar payoff and risk profile.
We say similar, but not 100% identical.
Investor Betty has a slightly lower maximum loss than Investor Adam:
Investor Betty’s max loss would occur when QQQ goes to zero.
In that case, Investor Betty can exercise the $ 560 put option to receive $560 per share.
Investor Betty max loss = $56,000 – $57,857 = -$1857
Recall that Investor Adam’s max loss is -$2065.
Why does Investor Betty have a lower max risk than Investor Adam by about $208?
This is the “free money” that the market is giving to Investor Betty because she is fronting $57,857 of debit to be in this trade.
Investor Betty has tied up $57,857 of cash that could have been used elsewhere.
This is the “opportunity cost” of holding this trade for 34 days.
This is known as the “cost of carry,” which is the cost of holding an asset until a future date.
The market compensates Investor Betty for this extra “cost”.
Who says the market is not fair?
It is as if Investor Betty had lent the market $57,857 and the market gave back a bit of interest in return.
As a general principle, if you have a debit option position, the market will “give you back” some “interest”.
If you have a credit position, you pay up a bit of “interest”.
However, in a typical options position, this interest is too small to even notice.
It becomes noticeable only when we replace a long option with its stock and equivalent put, which significantly increases the debit.
How much is this interest?
It is about the Federal Fund Rate or the risk-free rate of return.
Generally, the risk-free rate (as measured by treasury bills) closely tracks the fed funds rate.
In this example, a $208 return on $57,857 of capital over one month is approximately a 4% annualized return, close to the current risk-free rate of return as measured by the 10-Year Treasury rate.
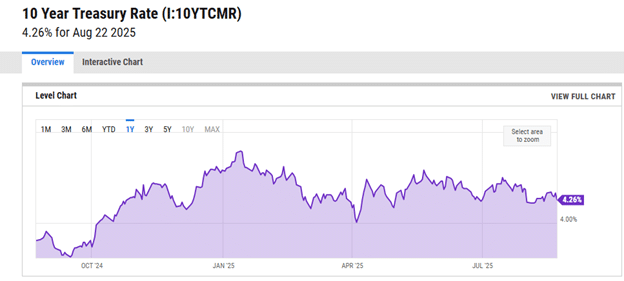
Source: ycharts.com
Taking the example further, suppose Investor Adam constructs a standard at-the-money butterfly with call options:
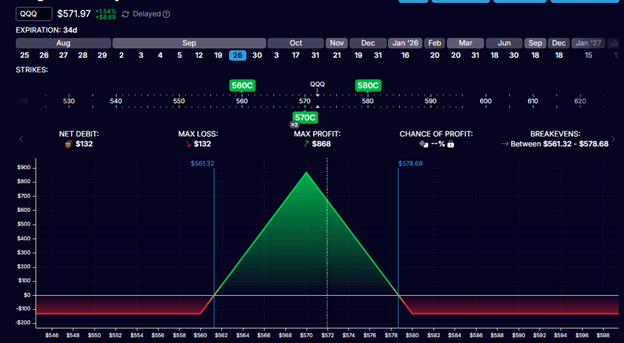
Buy one September 26 QQQ 580 call @ $7.78
Sell two September 26 QQQ 570 call @ $13.56 each
Buy one September 26 QQQ 560 call @ $20.65
Net debit: $132
Max risk: $132
Investor Betty builds the same trade, but replaces the 560-call option with 100 shares of QQQ plus an $560-strike put option.
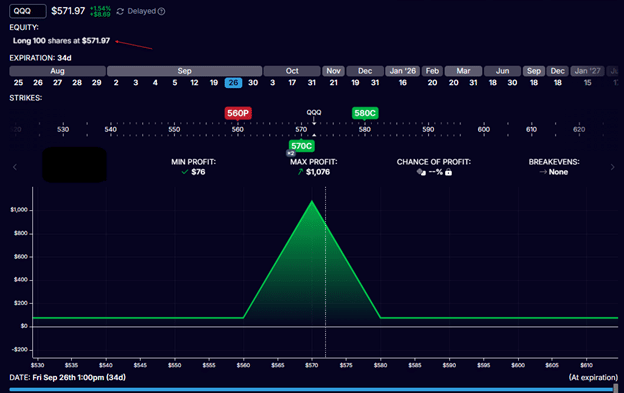
Buy 100 shares of QQQ @ $571.97 per share
Buy one September 26 QQQ 580 call @ $7.78
Sell two September 26 QQQ 570 call @ $13.56 each
Buy one September 26 QQQ 560 put @ $6.60
Net debit: -$55,924
Max risk: $0
Worst case: Profit of $76
Best case: Profit of $1076
In the worst-case scenario, when QQQ goes to zero, all the call options and shares become worthless.
The $560-strike put option would result in a loss of $56,000, which is $76 more than the investor had initially invested in the trade ($55,924).
Therefore, the trade can not lose money – as long as it is held to expiration.
The trade can experience a drawdown at some point during the trade.
And if the investor had exited the position at that time, a real loss would have been realized.
In the worst-case scenario, a $76 return on $55,924 of capital over 34 days is a 1.5% annualized return.
Because 76 / 55924 * 365 / 34 = 1.5% annualized
Yes, this is less than the risk-free rate of return of 4%, which the investor could obtain simply by buying some BIL.
However, if the investor is able to time and place the butterfly in such a way that the price ends up inside the expiration graph tent, the investor may be able to achieve much higher returns – perhaps not the maximum gain of $1076, but perhaps $400 out of it.
In that case:
400 / 55924 * 365 / 34 = 7.6% annualized
The overall annual return of the investor will vary depending on the skill in reading where the asset price will go, as well as trade management skills (when to exit).
If done well, the investor can make more than the risk-free rate.
If done poorly, the investor would be better off investing in treasury bills.
On average, the risk-fee rate is likely to be achieved.
But with nothing to lose, the investor can safely aim for a higher return.
Psychologically, the investor is also able to hold these trades longer to reap the larger profits that come into the butterfly only when it gets closer to expiration.
Why is Investor Betty able to get a risk-free trade, and Investor Adam is not?
Because Investor Betty is willing to put up $55,924 of capital, Investor Adam only put up $132.
If Investor Adam is willing to put the remaining $55,792 into the BIL treasury ETF (returning about 4% annually), then Investor Adam would have reaped $208 from the risk-free interest rate:
$55792 x 0.04 x 34 / 365 = $208
This would have more than covered the max loss of the butterfly plus an additional $76 – nearly exactly as Investor Betty.
If you group the legs of the above trade like this:
Bear call spread:
Buy one September 26 QQQ 580 call @ $7.78
Sell one September 26 QQQ 570 call @ $13.56
Options Collar:
Sell one September 26 QQQ 570 call @ $13.56
Buy 100 shares of QQQ @ $571.97
Buy one September 26 QQQ 560 put @ $6.60
It is really just an options collar with a bear call spread added.
This is what the option collar looks like:
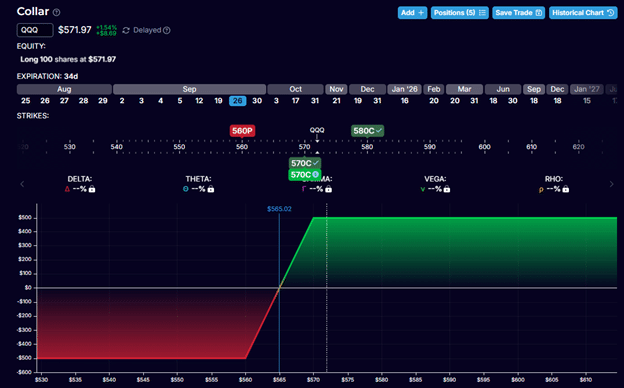
By itself, it is not risk-free. However, selling the bear call spread generates enough credit to make it risk-free.
In the above example, we have two short calls at $570.
Having short calls obligates the seller to sell 100 shares of QQQ whenever the other party requests it.
The other party is likely to ask for it close to the Ex-Dividend date when QQQ will pay out a dividend to people who own the shares before the ex-dividend date.
In the event that one short call is exercised, the 100 shares of QQQ will be called away, leaving a position with directional risk.
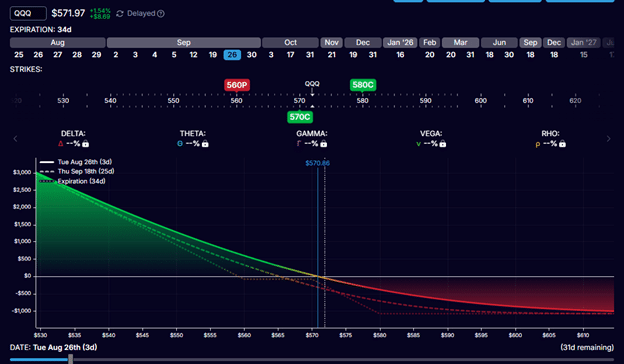
If both short calls are exercised, the investor will be short 100 shares of QQQ:
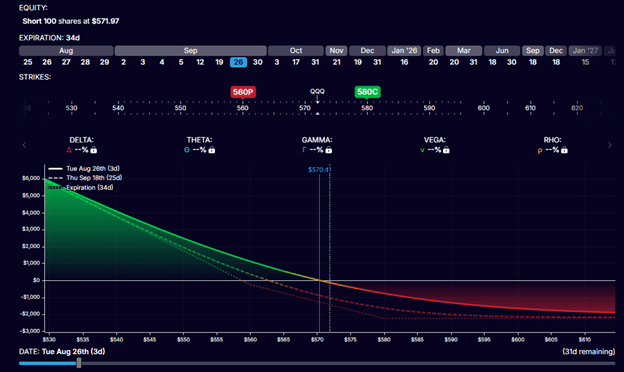
Leaving the position with directional risk (until the investor notices and closes out the entire position).
You can trade risk-free if you have enough capital to generate enough risk-free interest to offset any potential loss in a defined-risk trade.
This also means that these risk-free trades will NOT work in a zero-interest-rate environment (which we have had in the past).
The final caveat is that there is a low-probability risk of the short options being assigned early.
We hope you enjoyed this article on risk-free trades using put-call parity.
If you have any questions, send an email or leave a comment below.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.

